Um set é um tipo de dados de coleção não ordenado iterável, mutável e sem elementos duplicados. A classe de sets do Python representa a noção matemática de um conjunto. A principal vantagem de usar um conjunto, ao contrário de uma lista, é que ele possui um método altamente otimizado para verificar se um elemento específico está contido no conjunto. Isso se baseia em uma estrutura de dados conhecida como tabela hash. Como os conjuntos são desordenados, não podemos acessar os itens usando índices como fazemos nas listas.
# Programa python para demonstrar
# o uso de sets
# O mesmo que {"a", "b", "c"}
myset = set(["a", "b", "c"])
print(myset)
# Adiciona elementos ao conjunto (set)
myset.add("d")
print(myset)
Resultado>
{'c', 'b', 'a'}
{'d', 'c', 'b', 'a'}
Conjuntos Congelados (Frozen sets)
Conjuntos congelados em Python são objetos imutáveis que suportam apenas métodos e operadores que produzem um resultado sem afetar o conjunto ou conjuntos congelados aos quais são aplicados. Embora os elementos de um conjunto possam ser modificados a qualquer momento, os elementos do conjunto congelado permanecem os mesmos após a criação. Se nenhum parâmetro for passado, ele retornará um conjunto congeloda vazio.
# Programa Python para demonstrar diferenças
# entre conjunto normal e congelado
# o mesmo que {"a", "b","c"}
normal_set = set(["a", "b","c"])
print("Conjunto normal")
print(normal_set)
# Conjunto congelado
frozen_set = frozenset(["e", "f", "g"])
print("\nConjunto congelado")
print(frozen_set)
# Descomentar abaixo da linha causaria um erro, pois
# estamos tentando adicionar um elemento a um conjunto congelado
# frozen_set.add("h")
Resultado:
Conjunto normal
{'b', 'c', 'a'}
Conjunto congelado
frozenset({'e', 'g', 'f'})
Funcionamento interno do set
Isso se baseia em uma estrutura de dados conhecida como tabela hash. Se vários valores estiverem presentes na mesma posição de índice, o valor será anexado a essa posição de índice para formar uma Lista vinculada. Em, Python Sets são implementados usando dicionário com variáveis fictícias, onde a chave é o conjunto de membros com maiores otimizações para a complexidade do tempo.
Definir implementação:
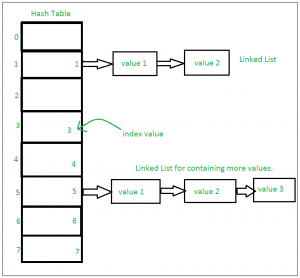
Conjuntos com várias operações em um único HashTable:
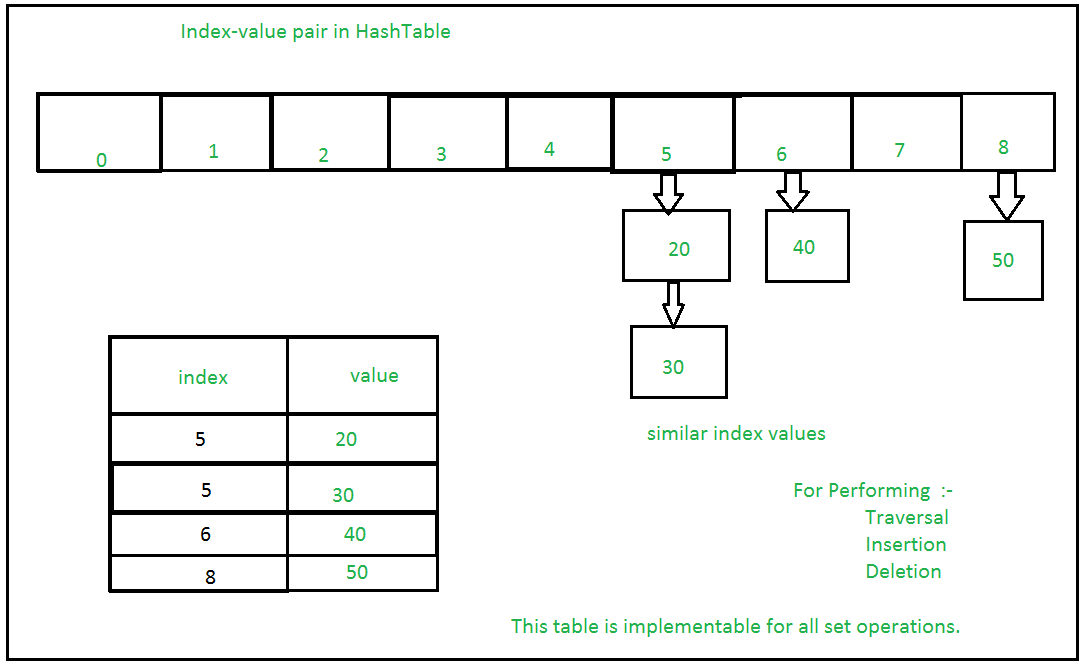
Métodos dos conjuntos em python
Adicionando elementos
A inserção no conjunto é feita por meio da função set.add(), onde um valor de registro apropriado é criado para armazenar na tabela hash. O mesmo que verificar um item, ou seja, O(1) em média. No entanto, na pior das hipóteses, pode se tornar O(n).
# programa python para demonstrar
# a adição de um novo elemento num conjunto
# Cria um conjunto
people = {"Jay", "Idrish", "Archi"}
print("Pessoas:", end=" ")
print(people)
# Isso vai adicionar Daxit ao conjunto
people.add("Daxit")
# adicionando elementos ao
# conjunto usando um interador
for i in range(1, 6):
people.add(i)
print("\nConjunto depois de adicionar os elementos:", end=" ")
print(people)
Resultado:
Pessoas: {'Archi', 'Idrish', 'Jay'}
Conjunto depois de adicionar os elementos: {1, 2, 3, 4, 5, 'Daxit', 'Idrish', 'Archi', 'Jay'}
União
Dois conjuntos podem ser mesclados usando a função union() ou o operador |. Ambos os valores da Tabela Hash são acessados e percorridos com a operação de mesclagem executada neles para combinar os elementos, ao mesmo tempo em que as duplicatas são removidas. A complexidade de tempo disso é O(len(s1) + len(s2)) onde s1 e s2 são dois conjuntos cuja união precisa ser feita.
# programa python para demonstrar
# a união de dois conjuntos
people = {"Jay", "Idrish", "Archil"}
vampires = {"Karan", "Arjun"}
dracula = {"Deepanshu", "Raju"}
# união usando a função union()
population = people.union(vampires)
print("Usando a função union")
print(population)
# usando o operador |
population = people | dracula
print("\nUnião usando o operador '|'")
print(population)
Interseção
Isso pode ser feito por meio de intersection() ou operador &. Elementos comuns são selecionados. Eles são semelhantes à iteração sobre as listas Hash e combinam os mesmos valores em ambas as tabelas. A complexidade de tempo disso é O(min(len(s1), len(s2)) onde s1 e s2 são dois conjuntos cuja união precisa ser feita.
# programa python para demonstrar
# a interseção de dois conjuntos
set1 = set()
set2 = set()
for i in range(5):
set1.add(i)
for i in range(3,9):
set2.add(i)
# interseção usando a função
# intersection()
set3 = set1.intersection(set2)
print("interseção usando a função intersection()")
print(set3)
# interseção usando o operador &
set3 = set1 & set2
print("\ninterseção usando o operador &")
print(set3)
Resultado:
interseção usando a função intersection()
{3, 4}
interseção usando o operador &
{3, 4}
Diferença
Para encontrar a diferença entre os conjuntos. Semelhante para encontrar diferença na lista vinculada. Isso é feito por meio da função difference() ou pelo operador -. Complexidade de tempo para encontrar a diferença s1 - s2 é O(len(s1))
# programa para monstrar a diferença
# entre dois conjuntos
set1 = set()
set2 = set()
for i in range(5):
set1.add(i)
for i in range(3,9):
set2.add(i)
# diferença entre dois conjuntos
# usando a função difference()
set3 = set1.difference(set2)
print("Diferença entre dois conjuntos usando a função difference()")
print(set3)
# diferença entre dois conjuntos
# usando o operador '-'
set3 = set1 - set2
print("\nDiferença entre dois conjuntos usando o operador '-'")
print(set3)
Resultado:
{0, 1, 2}
Diferença entre dois conjuntos usando o operador '-'
{0, 1, 2}
Limpando um conjunto
O método Clear() esvazia todo o conjunto.
# programa python para demonstrar
# a como limpar um conjunto
set1 = {1,2,3,4,5,6}
print("Conjunto inicial:")
print(set1)
# Esse método vai limpar o conjunto
set1.clear()
print("\nConjunto depois de chamar a função clear():")
print(set1)
Resultado:
Conjunto inicial:
{1, 2, 3, 4, 5, 6}
Conjunto depois de chamar a função clear():
set()
No entanto, existem duas armadilhas principais nos conjuntos Python:
- O conjunto não mantém elementos em nenhuma ordem particular.
- Apenas instâncias de tipos imutáveis podem ser adicionadas a um conjunto Python.
Complexidade de tempo dos conjuntos
| Operação | Caso médio | Pior caso | Observações |
|---|---|---|---|
| x in s | O(1) | O(n) | |
| Union s|t | O(len(s)+len(t)) | ||
| Interseção s&t | O(min(len(s), len(t)) | O(len(s) * len(t)) | Troque “min” por “max” se t não é um conjunto |
| Várias interseções s1&s2&..&sn | (n-1)*O(l) where l is max(len(s1),..,len(sn)) | ||
| Diferença s-t | O(len(s)) |
Operadores do conjuntos
Conjuntos e conjuntos congelados suportam os seguintes operadores:
| Operadores | Observações |
|---|---|
| chave em s | verificação de contenção |
| Sem chave em s | sem verificação de contenção |
| s1 == s2 | s1 é equivalente a s2 |
| s1 != s2 | s1 não é equivalente a s2 |
| s1 <= s2 | s1 é um subconjunto de s2 |
| s1 < s2 | s1 é um subconjunto adequado de s2 |
| s1 >= s2 | s1 é um super conjunto de s2 |
| s1 > s2 | s1 é um superconjunto adequado de s2 |
| s1 | s2 | a união de s1 e s2 |
| s1 & s2 | a interseção de s1 e s2 |
| s1 – s2 | o conjunto de elementos em s1 mas não em s2 |
| s1 ˆ s2 | o conjunto de elementos precisamente em um de s1 ou s2 |
Snippet de código para ilustrar todas as operações Set em Python:
# programa para desmonstar o funcionamento
# dos conjuntos em python
# cria dois conjuntos
set1 = set()
set2 = set()
# Adicionando elementos ao conjunto set1
for i in range(1, 6):
set1.add(i)
# Adicionando elementos ao conjunto set2
for i in range(3, 8):
set2.add(i)
print("Set1 = ", set1)
print("Set2 = ", set2)
print("\n")
# união dos conjuntos set1 e set2
set3 = set1 | set2 # set1.union(set2)
print("União de Set1 & Set2: Set3 = ", set3)
# interseção de set1 e set2
set4 = set1 & set2# set1.intersection(set2)
print("Interseção de Set1 & Set2: Set4 = ", set4)
print("\n")
# Verificando a relação entre set3 e set4
if set3 > set4: # set3.issuperset(set4)
print("Set3 é um super conjunto de Set4")
elif set3 < set4: # set3.issubset(set4)
print("Set3 é um subconjunto de Set4")
else: # set3 == set4
print("Set3 é o mesmo que Set4")
# mostrando a relação entre set4 e set3
if set4 < set3: # set4.issubset(set3)
print("Set4 é um subconjunto de Set3")
print("\n")
# diferença entre set3 e set4
set5 = set3 - set4
print("Elementos presentes em Set3 e não presentes em Set4: Set5 = ", set5)
print("\n")
# Verifica se set4 e set5 são conjuntos separados
if set4.isdisjoint(set5):
print("Set4 e Set5 não tem nada em comun\n")
# Remove todos os elementos do conjunto set5
set5.clear()
print("Depois de chamar a função clear() do objeto Set5: ")
print("Set5 = ", set5)
Resultado:
Set1 = {1, 2, 3, 4, 5}
Set2 = {3, 4, 5, 6, 7}
União de Set1 & Set2: Set3 = {1, 2, 3, 4, 5, 6, 7}
Interseção de Set1 & Set2: Set4 = {3, 4, 5}
Set3 é um super conjunto de Set4
Set4 é um subconjunto de Set3
Elementos presentes em Set3 e não presentes em Set4: Set5 = {1, 2, 6, 7}
Set4 e Set5 não tem nada em comun
Depois de chamar a função clear() do objeto Set5:
Set5 = set()
Artigo escrito por nikhilaggarwal3 e traduzido por Acervo Lima de Sets in Python
0 comentários:
Postar um comentário